Sine definition, a cornerstone of trigonometry, holds the key to unlocking a realm of mathematical wonders. Defined as the ratio of the opposite side to the hypotenuse in a right triangle, sine plays a pivotal role in shaping our understanding of angles, distances, and wave patterns.

Beyond its theoretical underpinnings, sine finds practical applications in diverse fields, from physics and engineering to music and architecture. Its versatility stems from its ability to model periodic phenomena, making it an indispensable tool for analyzing and predicting real-world events.

Define the Sine Function

The sine function is a fundamental trigonometric function that describes the vertical displacement of a point moving along a circular path. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.

Mathematically, the sine of an angle θ is given by the formula:

sin(θ) = opposite / hypotenuse

Applications of Sine in Real-World Scenarios, Sine definition

• Physics: Calculating the trajectory of projectiles, determining the period of a pendulum, and analyzing wave patterns.
• Engineering: Designing bridges, calculating the strength of materials, and determining the stability of structures.
• Music: Determining the pitch and frequency of musical notes.

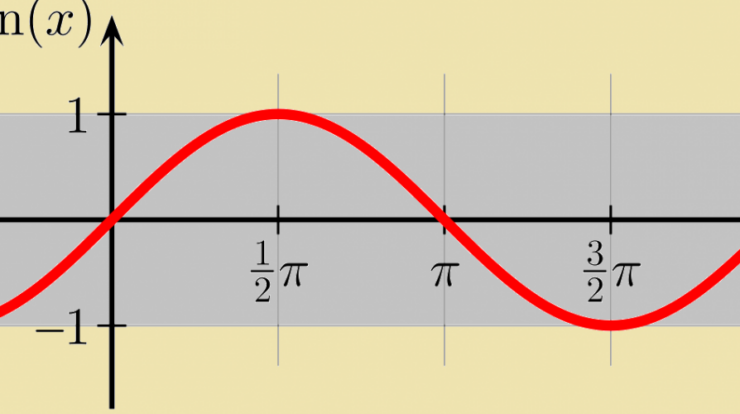
Graphing Sine Functions

A sine wave is a graphical representation of the sine function. It is characterized by a smooth, undulating pattern that repeats itself at regular intervals.

Key features of a sine graph include:

• Amplitude: The maximum displacement from the center line.
• Period: The distance between two consecutive peaks or troughs.
• Phase shift: The horizontal displacement of the graph from the origin.

Properties of Sine Functions

• Periodicity: Sine functions repeat their values at regular intervals called periods.
• Symmetry: Sine functions are odd functions, meaning they are symmetric about the origin.
• Boundedness: Sine functions are bounded between -1 and 1.

Applications of Sine in Calculus

Sine functions play a crucial role in calculus:

• Differentiation: The derivative of the sine function is the cosine function.
• Integration: The integral of the sine function is the negative cosine function.
• Solving real-world problems: Sine functions are used to find extrema, calculate areas, and solve differential equations.

Summary: Sine Definition

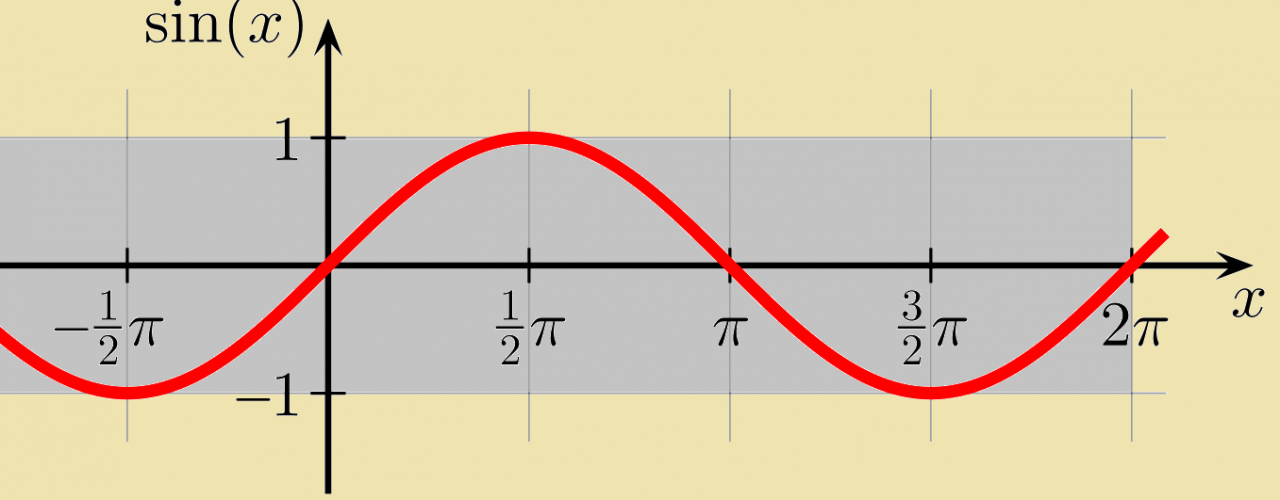
In conclusion, sine definition serves as a gateway to comprehending the intricate tapestry of trigonometry. Its applications extend far beyond the classroom, permeating various scientific and artistic disciplines. As we delve deeper into the properties and uses of sine, we gain a profound appreciation for its transformative power in shaping our world.

Commonly Asked Questions

What is the formula for sine?

sin(θ) = opposite/hypotenuse

How is sine related to other trigonometric functions?

Sine is one of the three main trigonometric functions, along with cosine and tangent. These functions are interrelated by the Pythagorean identity: sin²(θ) + cos²(θ) = 1.

What are some real-world applications of sine?

Sine is used in a wide range of fields, including physics, engineering, music, and architecture. It is used to calculate angles, distances, and wave patterns, among other things.